BOB version 1.2 [was CC Greasemonkey script - unofficial]

[andreweberman]

How about just a chart then? I know there are charts you can find online (or do yourself with out to much difficulty). Have a on/off switch which pulls up a spread sheet.

[chewyman]

Does anybody know what the asterisks or dash mean in this script? There are 1 - 3 asterisks or a single '-' after the territories counter. What does this represent?

[stocksr]

Does anybody know what the asterisks or dash mean in this script? There are 1 - 3 asterisks or a single '-' after the territories counter. What does this represent?

Number of territories is followed by a hyphen; '-' or one to three asterisks; '*'. The number of asterisks indicates the number of territories the player must lose to reduce the armies due by one. A hyphen indicates that the number of armies due cannot be reduced further by simply losing territories.

Has anybody read the help text? Is it obvious enough? How can we make it better?

[chewyman]

Does anybody know what the asterisks or dash mean in this script? There are 1 - 3 asterisks or a single '-' after the territories counter. What does this represent?

Number of territories is followed by a hyphen; '-' or one to three asterisks; '*'. The number of asterisks indicates the number of territories the player must lose to reduce the armies due by one. A hyphen indicates that the number of armies due cannot be reduced further by simply losing territories.

Has anybody read the help text? Is it obvious enough? How can we make it better?

Makes sense I suppose, but nobody actually reads that sort of thing. Could you maybe make it into a separate column of something?

[stocksr]

1) The calculations are accomplished through recursion (I believe) so it's a computationally expensive operation. If you get up in the range of more than 50 armies it becomes a slow operation. I'm not sure it's the sort of thing you want running whenever a user picks a country to attack in a drop down list.

Ok so we make it a button next to the attack button that pops up the results.

2) The main reason I use the battle odds calculator (Gambit) is to calculate my odds of success for eliminating one of my opponents. That is, I identify an attacking force and then a comma-separated list of the defender's remaining armies. The user interface suggested above wouldn't really support this use.

Interesting... I don't think we could do this.

3) There's no callable interface to either the Gambit or Bartell battle odds calculators, so one would have create a battle odds calculator from scratch. Since I'm basically lazy I'm not sure I'd want to tackle this. If someone wanted to pursue this I could offer some suggestions and ideas on how to go about it. [Basically there are six attacks (3v2, 3v1, 2v2, 2v1, 1v1, 1v2) for which the probabilities are known and it's possible to reduce any attack to a combination of these known attack probabilities.]

Could you provide links to these two so that I can check them out.

4) As an alternative, perhaps you could offer a link to a battle odds calculator on the game page. I would suggest the Gambit one. As a practical matter if I'm going to use Auto-Attack (which I don't by the way) I would be willing to click on the link to the Gambit calculator, enter my armies and the defender's armies and click calculate, before using the Auto-Attack button.

Again what is the link?

5) Both the Gambit and Bartell calculators are capped at a certain number of armies. Bartell is limited to 50 armies. Not sure what the limit for Gambit is, but it is limited also. There might be a very good reason for these limits as the calculation may take an unacceptably long time if they are exceeded.

Is there any less exact but faster calculation we could make, E.G assume that the attacker loses, 4 armies for every 5 defender - or what ever the average is.

[poo-maker]

http://gamesbyemail.com/Games/Gambit/BattleOdds? - gambit battle odds calculator

[tahitiwahini]

Could you provide links to these two so that I can check them out.

4) As an alternative, perhaps you could offer a link to a battle odds calculator on the game page. I would suggest the Gambit one. As a practical matter if I'm going to use Auto-Attack (which I don't by the way) I would be willing to click on the link to the Gambit calculator, enter my armies and the defender's armies and click calculate, before using the Auto-Attack button.

Again what is the link?

5) Both the Gambit and Bartell calculators are capped at a certain number of armies. Bartell is limited to 50 armies. Not sure what the limit for Gambit is, but it is limited also. There might be a very good reason for these limits as the calculation may take an unacceptably long time if they are exceeded.

Is there any less exact but faster calculation we could make, E.G assume that the attacker loses, 4 armies for every 5 defender - or what ever the average is.

Gambit: http://gamesbyemail.com/Games/Gambit/BattleOdds

Bartell: http://bartell.org/risk/riskodds.shtml

Yes, there probably is a way to arrive at an less exact estimate, along the lines that you suggest. When you start getting massive attacks, e.g., 30v25, it's really mostly 3v2 dice attacks so in that case we could probably identify the estimate as approximate and ignore what happens at the tail end of the attack sequences where the odds become less favorable to the attacker.

This brings up a topic that I haven't figured out the answer for yet so I'll put it out there for others to comment on:

It's a general question but I'll give it a specific instance if that's helpful.

Let's assume all territories have 3 armies from the initial deployment.
You're deploying three armies on your first turn and you want to know if it's better to deploy all three on the same country adjacent to the target or one on each of three countries adjacent to the target. In other words, is a 6v3 attack more likely to be successful than three 4v3 attacks executed sequentially.

The odds for the 6v3 attack being successful are 77%, but what are the odds that the three 4v3 attacks will be successful. The odds that one 4v3 attack will be successful are 47% but you get three tries at making the 47% and only one try at the 77%. So which is better?

The general question is how to mathematically combine probabilities in that way. It may be obvious, but so far it's stumped me.

[stocksr]

Thanks for the links.

It's a general question but I'll give it a specific instance if that's helpful.

Let's assume all territories have 3 armies from the initial deployment.
You're deploying three armies on your first turn and you want to know if it's better to deploy all three on the same country adjacent to the target or one on each of three countries adjacent to the target. In other words, is a 6v3 attack more likely to be successful than three 4v3 attacks executed sequentially.

The odds for the 6v3 attack being successful are 77%, but what are the odds that the three 4v3 attacks will be successful. The odds that one 4v3 attack will be successful are 47% but you get three tries at making the 47% and only one try at the 77%. So which is better?

The general question is how to mathematically combine probabilities in that way. It may be obvious, but so far it's stumped me.

FROM:
http://philosophy.hku.hk/think/stat/node5.php

Using the probability of each attack NOT winning = 53%
the probability of none of them winning is
not A X not B X not C = 0.148877%

making the probability of one of them winning 99.851123%

[yeti_c]

FROM:
http://philosophy.hku.hk/think/stat/node5.php

Using the probability of each attack NOT winning = 53%
the probability of none of them winning is
not A X not B X not C = 0.148877%

making the probability of one of them winning 99.851123%

Or about 50/50 if it's me!!!

C.

[stocksr]

FROM:
http://philosophy.hku.hk/think/stat/node5.php

Using the probability of each attack NOT winning = 53%
the probability of none of them winning is
not A X not B X not C = 0.148877%

making the probability of one of them winning 99.851123%

I should just add that there is a 50% chance of my maths being wrong as well

[tahitiwahini]

FROM:
http://philosophy.hku.hk/think/stat/node5.php

Using the probability of each attack NOT winning = 53%
the probability of none of them winning is
not A X not B X not C = 0.148877%

making the probability of one of them winning 99.851123%

I should just add that there is a 50% chance of my maths being wrong as well

Very interesting link you posted; I had been looking for something like that.

However, I'm not sold on the result although I must admit you seem to have followed the example given and I don't fault your methodology.

99.851123% seems awfully high to me. That basically makes it a lead pipe cinch that you're going to win.

Here's my informal reasoning about why that just doesn't seem right. A 6v3 army attack translates into a 5v3 dice attack, and the odds for success in such an attack are 76.93749%.

Let's look at the three 4v3 army attacks. How many attacking armies are really participating in the series of three attacks? Well, 4*3=12, attacking armies are participating in the attack. I think everyone will concede that three 4v3 army attacks is very unlikely to be better than a 12v3 army attack. The reason for this is that the 12v3 army attack has 5 guaranteed 3v2 dice attacks (namely: 12v3, 10v3, 8v3, 6v3, 4v3 army attacks if in the worst case the attacker loses 2 armies with every attack) while the three 4v3 army attacks have only 3 guaranteed 3v2 dice attacks (namely: 4v3, 4v3, and 4v3). So, what are the odds of a successful 12v3 army attack? Translated into a 11v3 dice attack they are 98.83882%. So in this case where we would expect a 12v3 attack to be superior to three 4v3 attacks it turns out that the 12v3 attack has a 1.012103% lesser chance of success. I think this makes the 99.851123% figure suspect.

It's actually worse than that because since you must subtract one army from each country participating in the three 4v3 army attacks there are really only (4-1)*3=9 armies participating in the attack. So for the same rationale as above we would rightfully expect that a (9+1)v3 army attack to be better than three 4v3 army attacks. The 10v3 army attack translates into a 9v3 dice attack which has odds of success of 96.69917%, which is 3.151953% less than the 99.851123% figure (for success in three 4v3 army attacks). This makes the 99.851123% figure look even more suspect.

In fact, not until a 14v3 dice attack (or 15v3 army attack) do we get odds for success higher than 99.851123% and surely three 4v3 army attacks cannot be better than a 14v3 army attack.

So something is wrong with the 99.851123% figure, but I'm still stumped about the right way to go about calculating it.

LOL, so my last ditch effort was to check your math, which I should have done in the first place (especially after your warning).

not A X not B X not C = 0.53 * 0.53 * 0.53 = 0.148877 = 14.8877%

making the probability of one of them winning 100% - 14.8877% = 85.1123%, which is a much more believable figure.

So your methodology was correct and I now have the answer to my question: it is better (8.17481% better) to make three 4v3 army attacks than a single 6v3 army attack.

Thanks.

[yeti_c]

Shit me - now that is good to hear... I shall use this technique in the future...

So does this also mean... a 5vs3 and a 4vs3 is better than one 6vs3? (If you only have 2 territories attacking?

C.

[tahitiwahini]

Shit me - now that is good to hear... I shall use this technique in the future...

So does this also mean... a 5vs3 and a 4vs3 is better than one 6vs3? (If you only have 2 territories attacking?

C.

Yes, 5v3 army attack is successful 64.16229% of the time, 4v3 army attack is successful 47.02511% of the time, so

(1 - 0.64.16229) * (1 - 0.47.02511) = 18.9849% of the time neither attack will be successful, which conversely means 81.0150% of the time one of the attacks will succeed.

So, 5v3 and 4v3 are 4.093% worse than three 4v3 attacks, but 4.07751% better than a single 6v3 attack.

So, on initial deployment, placing 1 army on each of three territories adjacent to the target is optimal (85.1123% successful), placing 2 armies on one territory and one on another adjacent to the target is next best (80.0150% successful), and placing all three armies on a single territory adjacent to the target is least likely to be a successful strategy (76.93749% successful).

[stocksr]

So, on initial deployment, placing 1 army on each of three territories adjacent to the target is optimal (85.1123% successful), placing 2 armies on one territory and one on another adjacent to the target is next best (80.0150% successful), and placing all three armies on a single territory adjacent to the target is least likely to be a successful strategy (76.93749% successful).

Hang on, are we talking about using
[4,4,4]v[3] (one target)
or
4v3, 4v3, 4v3 (three targets)

My maths (well the idea if not the implementation ) was based on the three targets aka (unrelated events)

[stocksr]

Shit me - now that is good to hear... I shall use this technique in the future...

So does this also mean... a 5vs3 and a 4vs3 is better than one 6vs3? (If you only have 2 territories attacking?

C.

5+4 > 6
so your odds must go up as well.

the actual question should be, which is better

[6,3] v 3
or
[5,4] v 3


also we are assuming that the ONLY goal is to get the territory NO MATTER the cost.

[yeti_c]

Shit me - now that is good to hear... I shall use this technique in the future...

So does this also mean... a 5vs3 and a 4vs3 is better than one 6vs3? (If you only have 2 territories attacking?

C.

5+4 > 6
so your odds must go up as well.

the actual question should be, which is better

[6,3] v 3
or
[5,4] v 3


also we are assuming that the ONLY goal is to get the territory NO MATTER the cost.

No no...

I mean say you start and you have two 3's next to a territory...

Do you deploy 1 and a 2 to the territories or all 3 to one territory.

C.

[tahitiwahini]

Shit me - now that is good to hear... I shall use this technique in the future...

So does this also mean... a 5vs3 and a 4vs3 is better than one 6vs3? (If you only have 2 territories attacking?

C.

5+4 > 6
so your odds must go up as well.

the actual question should be, which is better

[6,3] v 3
or
[5,4] v 3


also we are assuming that the ONLY goal is to get the territory NO MATTER the cost.

No no...

I mean say you start and you have two 3's next to a territory...

Do you deploy 1 and a 2 to the territories or all 3 to one territory.

C.

Well, I think I was answering the question yeti_c was asking, so I think my answer stands about which is better, but I'm no longer confident in the numbers I gave.

stocksr's correct that the only consideration is to conquer the country. So it may be the case that while my proposed optimal deployment gives you the highest likelihood of conquering the country it does so possibly at a higher cost in terms of armies lost in the attack. (In other words, because more armies are involved in the attack your overall likelihood of success is higher but you may take greater loses because you have more armies involved in the attack.)

Also, stocksr makes a good point about the independence of the 4v3 attacks. They aren't independent. It's obvious that you would want to make your attacks in this order: 4v3, 4(from another territory)v(3-a) where a is the number of armies lost in the first attack, 4(from the third territory)v(3-a-b) where b is the number of armies lost in the second attack. Unfortunately, the way I'm calculating the odds is by assuming that I do a 4v3 attack which I pursue until successful or I can't attack any more. I properly assign a 47% chance to the success of that attack. Then I make another 4v3 attack, except at this point there may no longer be 3 defending armies after the first attack series, so I am probably not justified in assigning a 47% chance of success of the second attack. The chance of success should probably be higher than that, taking into account the damage potential damage done to the defender from the first attack. In any case, that's not the way I would make the attacks anyway -- I would always attack from the country that had the most armies, I would not attack from one country until success or failure and then move on to attack from the second country until success or failure. So I'm not calculating the odds the way I'd be making the attacks. Hence the odds I'm giving for successfully conquering the territory are probably lower than they should be.

So the problem remains how to calculate the probabilities properly for these kind of attacks.

So I guess I still think the deployment and attacks I recommend are the best way to go, I just can't provide a reliable measure of the likelihood of success other than to say it's probably higher than I indicated it was.

[cicero]

"Ouch my head hurts
Ouch my head hurts
Ouch my head hurts quite a bit"

(Sung to the tune of your choosing.)


cicero

[haoala]

i just realised a BIG BIG GLITCH with this thing
since lack introduced the new rule where if someone deadbeats in a team, the troops and cards will be given to the next guy.
but this isnt counted in the script, and it becomes inaccurate
will somebody fix this?

[The1exile]

I just encountered a bug with this script.

See the bit about reds cards and cashins on this screenshot:



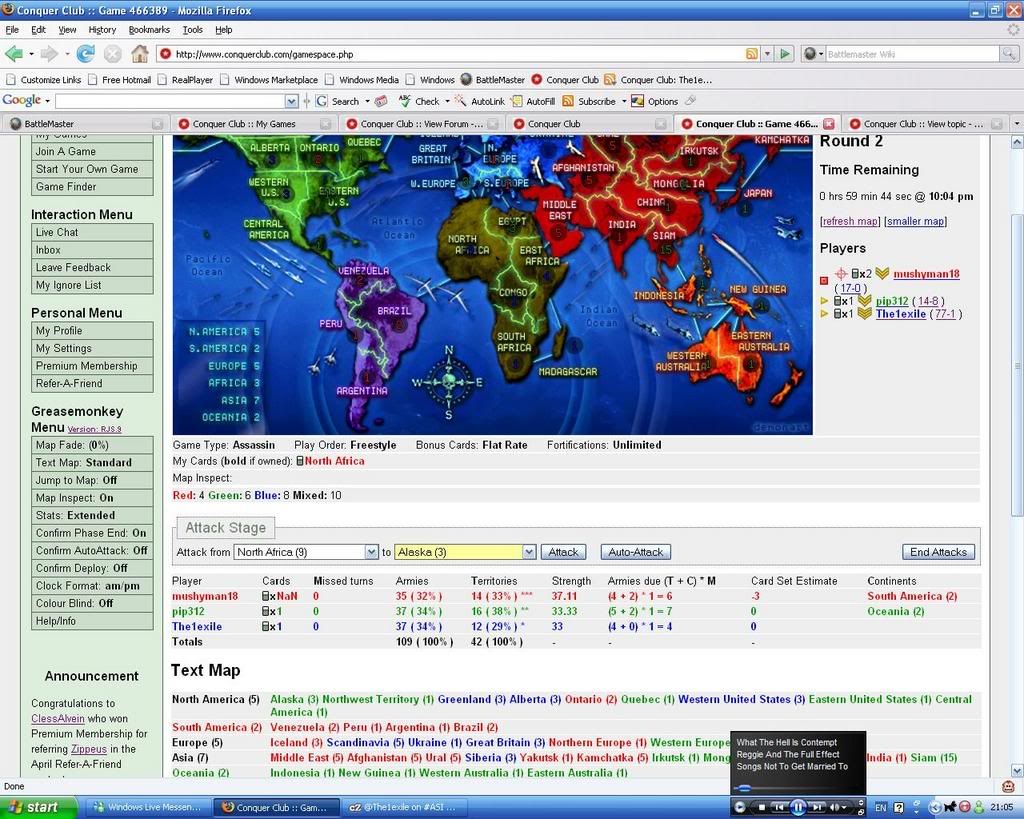
Not sure what triggered it.

[weirdbro]

I would assume its a problem with Assassin and the script. Whats the game number for that game?

[The1exile]

466389.

EDIT: it's in the title bar

[weirdbro]

Well, the game being over is a problem for looking for the glitch.

[tahitiwahini]

Well, the game being over is a problem for looking for the glitch.

Not necessarily. Let's say for the sake of argument it's not a BOB problem. Remember BOB relies on its inputs from parsing the game log. What if when the game log is looked at there's some problem with the accounting for red's cards? There's nothing BOB could do about that.

On the other hand the problem could be in BOB if the game log checks out OK.

After checking the game, it appears the game log is OK. At the point the screen capture was made (in Round 2) red should have had [edit] 2 cards [/edit], so it seems there might be something amiss with BOB. Interestingly it seems to have been a transient problem since BOB got back to being correct at the end of the game. I don't believe BOB has any memory, that is, it recalculates everything every time the screen is refreshed. What would have caused it to be confused parsing the game log during round 2 is rather mysterious.

[weirdbro]

It still gets cards from the log? I thought it switched to just reading from what CC says now that it was added.