I'm sorry but how are you getting this? How is it approaching it slower?TheProwler wrote:In your example, 9+ 0.9999... - 0.9999..., the first 0.9999... is approaching 1 just a wee bit slower than the second 0.9999....a.sub wrote:its common sense,ser stiefel wrote:Of course it is only true if you do the operation all the way out to the least significant digit.Army of GOD wrote:I always disagreed with this.
Until I read this:http://mathforum.org/dr.math/faq/faq.0.9999.htmllim_(m --> oo) sum_(n = 1)^m (9)/(10^n) = 1
0.9999... = 1
Thus x = 0.9999...
10x = 9.9999...
10x - x = 9.9999... - 0.9999...
9x = 9
x = 1.
9.9999... - 0.9999...
9+ 0.9999... - 0.9999...
9
unless u want to argue that something minus its self is not zero, in which case u shd prolly review basic math.
.999... = 1
Moderator: Community Team
Forum rules
Please read the Community Guidelines before posting.
Please read the Community Guidelines before posting.
-
Army of GOD
- Posts: 7192
- Joined: Tue Feb 24, 2009 4:30 pm
- Gender: Male
Re: .999... = 1
mrswdk is a ho
- TheProwler
- Posts: 354
- Joined: Mon Feb 12, 2007 9:54 am
- Gender: Male
- Location: Ontario, Canada
Re: .999... = 1
And that's the problem when dealing with irrational numbers and our imperfect system of depicting them using our standard numbering system.
We simply say
0.999... * 10 = 9.999...
And we are too happy to think that we understand it. So we merrily subtract 0.999... from 9.999... and think it equates to 9. Not that simple.
Think of it like this, instead: 0.9999... * 10 = 9.999...
Notice the four 9's after the decimal versus the three 9's. This is for illustrative purposes only, before you get too upset.
y = 1/x
As x approaches infinity, y approaches 0.
z = 1/(2x)
As x approaches infinity, z approaches 0.
But, y does not equal z.
Let's go back to the "proof" given above. (0.999... * 10 = 9.999..., etc.)
But let's not define x. Let's solve for x:
x * 10 = x + 9
You get x = 1. Try it.
Simple arithmetic for simple rational numbers.
Here's another example of mixing simple arithmetic with concepts like infinity:
a = b
a^2 = a*b
a^2-b^2 = a*b-b^2
(a+b)(a-b) = b(a-b)
(a+b) = b
a+a = a
2a = a
2 = 1
Please don't tell me you believe 1 equals 2.
We simply say
0.999... * 10 = 9.999...
And we are too happy to think that we understand it. So we merrily subtract 0.999... from 9.999... and think it equates to 9. Not that simple.
Think of it like this, instead: 0.9999... * 10 = 9.999...
Notice the four 9's after the decimal versus the three 9's. This is for illustrative purposes only, before you get too upset.
y = 1/x
As x approaches infinity, y approaches 0.
z = 1/(2x)
As x approaches infinity, z approaches 0.
But, y does not equal z.
Let's go back to the "proof" given above. (0.999... * 10 = 9.999..., etc.)
But let's not define x. Let's solve for x:
x * 10 = x + 9
You get x = 1. Try it.
Simple arithmetic for simple rational numbers.
Here's another example of mixing simple arithmetic with concepts like infinity:
a = b
a^2 = a*b
a^2-b^2 = a*b-b^2
(a+b)(a-b) = b(a-b)
(a+b) = b
a+a = a
2a = a
2 = 1
Please don't tell me you believe 1 equals 2.
El Capitan X wrote:The people in flame wars just seem to get dimmer and dimmer. Seriously though, I love your style, always a good read.
- SultanOfSurreal
- Posts: 97
- Joined: Thu Jul 03, 2008 3:53 am
- Gender: Male
Re: .999... = 1
MAN i am glad i bumped this threadTheProwler wrote:And that's the problem when dealing with irrational numbers and our imperfect system of depicting them using our standard numbering system.
We simply say
0.999... * 10 = 9.999...
And we are too happy to think that we understand it. So we merrily subtract 0.999... from 9.999... and think it equates to 9. Not that simple.
Think of it like this, instead: 0.9999... * 10 = 9.999...
Notice the four 9's after the decimal versus the three 9's. This is for illustrative purposes only, before you get too upset.
y = 1/x
As x approaches infinity, y approaches 0.
z = 1/(2x)
As x approaches infinity, z approaches 0.
But, y does not equal z.
Let's go back to the "proof" given above. (0.999... * 10 = 9.999..., etc.)
But let's not define x. Let's solve for x:
x * 10 = x + 9
You get x = 1. Try it.
Simple arithmetic for simple rational numbers.
Here's another example of mixing simple arithmetic with concepts like infinity:
a = b
a^2 = a*b
a^2-b^2 = a*b-b^2
(a+b)(a-b) = b(a-b)
(a+b) = b
a+a = a
2a = a
2 = 1
Please don't tell me you believe 1 equals 2.
Re: .999... = 1
TheProwler wrote:And that's the problem when dealing with irrational numbers and our imperfect system of depicting them using our standard numbering system.
We simply say
0.999... * 10 = 9.999...
And we are too happy to think that we understand it. So we merrily subtract 0.999... from 9.999... and think it equates to 9. Not that simple.
Think of it like this, instead: 0.9999... * 10 = 9.999...
Notice the four 9's after the decimal versus the three 9's. This is for illustrative purposes only, before you get too upset.
y = 1/x
As x approaches infinity, y approaches 0.
z = 1/(2x)
As x approaches infinity, z approaches 0.
But, y does not equal z.
for this example ... wrong, y DOES equal z when x equal infinity. use ur own limits
y as x --> infinity = 0
z as x --> infinity = 0
Let's go back to the "proof" given above. (0.999... * 10 = 9.999..., etc.)
But let's not define x. Let's solve for x:
x * 10 = x + 9
You get x = 1. Try it.
Simple arithmetic for simple rational numbers.
Here's another example of mixing simple arithmetic with concepts like infinity:
a = b
a^2 = a*b
a^2-b^2 = a*b-b^2
(a+b)(a-b) = b(a-b)
(a+b) = b
a+a = a
2a = a
2 = 1
ur making a vital error of diving by 0, that is complete different, where do i divide by zero in my proof? QED
Please don't tell me you believe 1 equals 2.
- MeDeFe
- Posts: 7831
- Joined: Thu Apr 06, 2006 2:48 am
- Location: Follow the trail of holes in other people's arguments.
Re: .999... = 1
0.999... does not "approach" anything. It is a number, it's fixed, not something you have to keep adding nines to.
saxitoxin wrote:Your position is more complex than the federal tax code. As soon as I think I understand it, I find another index of cross-references, exceptions and amendments I have to apply.
Timminz wrote:Yo mama is so classless, she could be a Marxist utopia.
- TheProwler
- Posts: 354
- Joined: Mon Feb 12, 2007 9:54 am
- Gender: Male
- Location: Ontario, Canada
Re: .999... = 1
When x equal infinity.a.sub wrote:for this example ... wrong, y DOES equal z when x equal infinity. use ur own limits
y as x --> infinity = 0
z as x --> infinity = 0
x never equals infinity.
So you are correct. never.
I using an example of where people look at Algebraic solutions and overlook simple facts. Facts like our numbering system can only show estimates of irrational numbers. And, therefore, precise calculations are flawed.a.sub wrote:ur making a vital error of diving by 0, that is complete different, where do i divide by zero in my proof? QED
El Capitan X wrote:The people in flame wars just seem to get dimmer and dimmer. Seriously though, I love your style, always a good read.
- TheProwler
- Posts: 354
- Joined: Mon Feb 12, 2007 9:54 am
- Gender: Male
- Location: Ontario, Canada
Re: .999... = 1
It is a concept. It is not a "fixed" number.MeDeFe wrote:0.999... does not "approach" anything. It is a number, it's fixed, not something you have to keep adding nines to.
As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life) unless you apply arithmetic to estimates (ie. numbers with repeating decimal places) and forget that you are dealing with estimates. That's the problem with all the "proofs" that have been submitted.
I don't believe anybody has stepped up and shown an example of where 0.999... will be the result of a mathematical problem that doesn't include a repeating sequence or a number with repeating decimals in it's definition. In other words, try producing a mathematical problem composed of rational numbers that results in 0.999... Try showing a real-world problem that results in 0.999....
This thread has been a great statement of the pomposity of some of the users here. This is an argument that intelligent people all over the world are having. And it hasn't been resolved to this day. Yet a handful of users on CC seem to think they can turn it into a simple popularity vote and because their "solutions" get a nod of approval by a few other users, they are satisfied that they are right, and anyone who opposes their thoughts are wrong and should be mocked. It's not really that way yet (in this revival of the thread), but it will be soon.
Here's a page where it is being discussed: http://en.wikipedia.org/wiki/User:ConMa ... ot_equal_1
At this point in time: The second last post is by a Humanities Major, which is kinda funny, because he identifies that this is theoretical stuff while the mathies want to argue that it is all very "real". The last post is by a guy that seems to think that approaching zero means equal to zero. A common misconception, it seems.
Here's a quick discussion on this subject from last year: http://www.physicsforums.com/archive/in ... 15017.html
It's pretty obvious that sometimes people will just have to agree to disagree. I think this is a matter of discerning the difference between being equal and that of approaching a limit. Others obviously disagree.
El Capitan X wrote:The people in flame wars just seem to get dimmer and dimmer. Seriously though, I love your style, always a good read.
Re: .999... = 1
i couldn't resist prowley, for old time's sake.
intents and purposes
if you need me i'll be nursing my semi
intents and purposes
if you need me i'll be nursing my semi
had i been wise, i would have seen that her simplicity cost her a fortune
- Lord and Master
- Posts: 64
- Joined: Tue Jul 31, 2007 3:38 pm
- Gender: Male
- Location: Wherever
Re: .999... = 1
TheProwler wrote:As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life) unless you apply arithmetic to estimates (ie. numbers with repeating decimal places) and forget that you are dealing with estimates. That's the problem with all the "proofs" that have been submitted.
I don't believe anybody has stepped up and shown an example of where 0.999... will be the result of a mathematical problem that doesn't include a repeating sequence or a number with repeating decimals in it's definition. In other words, try producing a mathematical problem composed of rational numbers that results in 0.999... Try showing a real-world problem that results in 0.999....
Yes, you are absolutely correct. We can say that the fraction 1/9 expressed as a decimal equals 0.111... so for someone to say that taking that and multiplying it by 9 gives 0.999... is talking complete rubbish as 9/9 most definitely equals 1. Mathematicians prefer to deal with fractions wherever possible as it keeps the equation/formula "purer", that is they don't lose any accuracy due to the decimal "approximation".
Anyway, anybody who genuinely thinks any given number can EVER equal another given number is clearly a cretin of the highest order and should simply be ignored where possible, beaten into submission with big sticks where not.

- SultanOfSurreal
- Posts: 97
- Joined: Thu Jul 03, 2008 3:53 am
- Gender: Male
Re: .999... = 1
TheProwler wrote:In other words, try producing a mathematical problem composed of rational numbers that results in 0.999... Try showing a real-world problem that results in 0.999....
.999... is a rational number
the ratio you can use to represent it is 1/1
Re: .999... = 1
Lord+Master wrote:TheProwler wrote:As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life) unless you apply arithmetic to estimates (ie. numbers with repeating decimal places) and forget that you are dealing with estimates. That's the problem with all the "proofs" that have been submitted.
I don't believe anybody has stepped up and shown an example of where 0.999... will be the result of a mathematical problem that doesn't include a repeating sequence or a number with repeating decimals in it's definition. In other words, try producing a mathematical problem composed of rational numbers that results in 0.999... Try showing a real-world problem that results in 0.999....
Yes, you are absolutely correct. We can say that the fraction 1/9 expressed as a decimal equals 0.111... so for someone to say that taking that and multiplying it by 9 gives 0.999... is talking complete rubbish as 9/9 most definitely equals 1. Mathematicians prefer to deal with fractions wherever possible as it keeps the equation/formula "purer", that is they don't lose any accuracy due to the decimal "approximation".
Anyway, anybody who genuinely thinks any given number can EVER equal another given number is clearly a cretin of the highest order and should simply be ignored where possible, beaten into submission with big sticks where not.
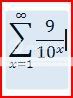
- MeDeFe
- Posts: 7831
- Joined: Thu Apr 06, 2006 2:48 am
- Location: Follow the trail of holes in other people's arguments.
Re: .999... = 1
Maybe one number can not equal another number, but considering that 0.999... and 1 are the same number I don't see that applying here.Lord+Master wrote:Yes, you are absolutely correct. We can say that the fraction 1/9 expressed as a decimal equals 0.111... so for someone to say that taking that and multiplying it by 9 gives 0.999... is talking complete rubbish as 9/9 most definitely equals 1. Mathematicians prefer to deal with fractions wherever possible as it keeps the equation/formula "purer", that is they don't lose any accuracy due to the decimal "approximation".
Anyway, anybody who genuinely thinks any given number can EVER equal another given number is clearly a cretin of the highest order and should simply be ignored where possible, beaten into submission with big sticks where not.
saxitoxin wrote:Your position is more complex than the federal tax code. As soon as I think I understand it, I find another index of cross-references, exceptions and amendments I have to apply.
Timminz wrote:Yo mama is so classless, she could be a Marxist utopia.
- Snorri1234
- Posts: 3438
- Joined: Wed Sep 12, 2007 11:52 am
- Location: Right in the middle of a fucking reptile zoo.
- Contact:
Re: .999... = 1
Indeed.MeDeFe wrote:Maybe one number can not equal another number, but considering that 0.999... and 1 are the same number I don't see that applying here.Lord+Master wrote:Yes, you are absolutely correct. We can say that the fraction 1/9 expressed as a decimal equals 0.111... so for someone to say that taking that and multiplying it by 9 gives 0.999... is talking complete rubbish as 9/9 most definitely equals 1. Mathematicians prefer to deal with fractions wherever possible as it keeps the equation/formula "purer", that is they don't lose any accuracy due to the decimal "approximation".
Anyway, anybody who genuinely thinks any given number can EVER equal another given number is clearly a cretin of the highest order and should simply be ignored where possible, beaten into submission with big sticks where not.
No it is a fixed number. It is simply "1" written in another way.It is a concept. It is not a "fixed" number.
"Some motherfuckers are always trying to ice skate uphill."
Duane: You know what they say about love and war.
Tim: Yes, one involves a lot of physical and psychological pain, and the other one's war.
Duane: You know what they say about love and war.
Tim: Yes, one involves a lot of physical and psychological pain, and the other one's war.
- sully800
- Posts: 4978
- Joined: Wed Jun 14, 2006 5:45 pm
- Gender: Male
- Location: Bethlehem, Pennsylvania
Re: .999... = 1
That's strange, because I use and see the number 1 all the time. In fact I think I use it more than any other number!TheProwler wrote:As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life)
Re: .999... = 1
am i being ignored here? here is an example where you get .9999999...sully800 wrote:That's strange, because I use and see the number 1 all the time. In fact I think I use it more than any other number!TheProwler wrote:As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life)
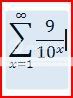
- sully800
- Posts: 4978
- Joined: Wed Jun 14, 2006 5:45 pm
- Gender: Male
- Location: Bethlehem, Pennsylvania
Re: .999... = 1
Oh, you are quite correct that you can get 0.999... by doing that infinite sum.a.sub wrote:am i being ignored here? here is an example where you get .9999999...
You can also get it by dividing 9 by 9. Or subtracting 1 from 2. Or subtracting 0.999... from 2.
Re: .999... = 1
I can't believe I wasted the last hour reading through this entire thread, or that I'm about to waste more time adding to it, but here we go...
First, for what it's worth, I have a BS in mathematics and a substantial amount of graduate level mathematics (though my PhD is in Optical Physics, so I don't have quite enough math-specific classes for a graduate degree in that field). I have also been a math teacher.
First, the easy one: e_i_pi was slightly off in his discussion of plank lengths as a counter example of nonexistance of infinitesimals. The reason is that the set of real numbers is dense - meaning that between any two distinct real numbers there exists at least one (and actually an infinite amount) of other distinct real numbers. This is not so in the physical world. Consider two different lengths: 1 plank length and 2 plank lengths. Those are clearly distinct lengths, but there is no measurable length that is strictly between the two.
Also, 0 is most definitely a number. It is a member of the sets of natural numbers, integers, rational number, real numbers, and complex numbers. It is essential to all of these number sets in order to provide a complete definition for the addition operation (it is the identity element with respect to addition in most number systems).
Now then, it is quite clear that Prowler doesn't understand the concept of infinity. But I think the problem he is having is that he is approaching mathematics from the computer programming side rather than from the abstract side (I do quite a bit of programming, so I think I understand why he's reaching the conclusions he is). The misconception is that 0.999... is either a series approaching some value, or that it is lacking in some way. It isn't either. It is an exact number with an exact value. Certainly the "..." gives our brains some trouble (and our computers even more trouble!), but it is a notation that has an exact value and an exact meaning. Likewise 2/infinity and 1/infinity are not limits in and of themselves. lim(1/x, x->inf) and lim(2/x, x->inf) are limits and are absolutely not the same as 1/infinity and 2/infinity. But also note that the two limits have the same value. It doesn't matter than one is smaller than the other for all values of x, both limits have the exact same value! If you want to take about the rate at which they approach 0, we can discuss derivatives, but the concept of interest is the value of 1/x "at infinity", and when we use the limit to express that, we find that it is exactly the same value as 2/x regardless of which one is getting there quicker. (I started to say "gets there first," but that has no meaning when both only get there at infinity anyway. Better to say they get there at the same time.)
It is true that infinity is not a real number, but it can be used as a number if done carefully (see Definition 2.2 - the extended real number system on page 23 of "Introductory Real Analysis by Dangello and Seyfried). The problem Prowler is having is in thinking that infinity+1 is larger than infinity. This is a necessary condition in order for 1 - 0.99999... > 0. However, it is a flawed premise, and I can provide you a proof using the concept of cardinality.
Cardinality is the size of a set of numbers - think of it as the number of numbers in a set. So the cardinality of the set {0,1} is 2, while the cardinality of {1,2,3} is 3. That two sets have the same cardinality is equivalent to the two sets having a mapping between them that is both "one-to-one" and "onto." In simplified terms, if I have two sets and I can provide a direct mapping between every element in one set to a distinct element in the other set and vice versa, the sets are said to have the same cardinality. For example, {1,2,3} is easily mapped to {1,2,5}. In some cases we can express the mapping as a convenient formula: {1,2,3} maps to {2,4,6} using the formula y=2x. Natural numbers is the set including 0 and all positive integers: {0,1,2,3,4,5,...}. What is the cardinality of this set? It is clearly infinite, and its cardinality of this set is called Aleph Null. Any set for which one can find an exact 1-to-1 mapping with the natural numbers is said to be "countable infinite" and has a cardinality of Aleph Null. Conversely, if you have a set that contains every natural number but for which it is impossible to map every one of its elements to a distinct natural number, this set has a larger cardinality.
Here's where things get really funny. Consider the set, A, which contains all the natural number (N), and the number -1. So, A = {-1,0,1,2,3,4,...}. If the cardinality of N is inifinite (Aleph Null), logic would suggest that the cardinality of A is (Aleph Null + 1). That would actually be incorrect. Consider the mapping: a=n-1. (Where a is a member of A and n is a member of N). For every single member a, there exists a corresponding member, n, and vice versa. This mapping is both 1-to-1 and onto. The two sets have the same cardinality, and infinity+1=infinity.
It is straightforward to show that the cardinality of the positive even integers is the same as the positive integers, and that the cardinality of all integers {...,-2,-1,0,1,2,3,...} is likewise the same (for some additional fun on all this, look up Hilbert's Hotel). Furthermore, it is possible to show that the set of rational numbers (all numbers that can be expressed as a/b where a,b are members of the set of integers) likewise has the same cardinality as the natural numbers. This is an extremely interesting result because the rational numbers are dense, while the natural numbers are not! On the other hand, the real numbers are dense but are uncountable (which was proved by Georg Cantor in 1874). The cardinality of the real numbers is believed to be Aleph 1 (think of it as the next larger value of infinity). I won't get into all the details. Real numbers have a larger cardinality than the naturals, and that cardinality is supposed to be the same as the cardinality of the so-called power set of the natural numbers, but this hypothesis can be neither proved nor disproved.
The point of all this is about the size of infinity. There are in fact multiple values of infinity (aleph null, aleph 1, aleph 2, ...), however, you don't increase the size of a set from one level to the next by simply adding a finite number of elements. Nor can you do it even by squaring the number of elements. It might be best to think of the relations between them as being on the order of the factorial operation. This isn't strictly valid, but it's convenient to think about the relative sizes in this way.
Now that I've explained all that (and clearly demonstrated a sufficient feel for the concept of infinity), let's go back to the original problem. It is a definition of real numbers that if two numbers are distinct, there exists some number (that is a member of the real numbers) strictly between them. Note that if a number is a member of the reals, it has to be represented as such either as a truncated or repeating decimal (in which case it is a rational number and can also be written as a fraction of integers) or as an infinite non-repeating decimal (in which case it is irrational and may not be written with perfect precision but can be written as an approximation with arbitrary precision). 0.9 and 1 are clearly distinct - 0.95 is strictly between them. 0.99 and 1 are distinct - 0.995 is strictly between them. The question is whether 0.99... and 1 are distinct. What possible real number can fall between them? The previous two examples might lend someone to suggest (and I've seen people on other forums try this) that 0.999...9995 could be somehow larger than 0.999... Yet this is simply impossible. This claim requires that you somehow be able to affect the infinity+1 digit without changing the infinity digit. Furthermore, 0.999...9995 really has no meaning except as a finite decimal, in which case it is actually less than 0.999...! Likewise, there is no such thing as 0.00.....001 except as a very small finite number. If you try to posit that there is such a number, you should be ready to explain what digit follows the 1! And if you try to work with the 0.999...995 once more, I'll ask you to name the digit that contains the 5, and I'll let my 0.999... have a 9 in that digit and another 9 for infinite digits beyond the one containing your 5. My number will be larger than yours and has no difference between it and 1.
First, for what it's worth, I have a BS in mathematics and a substantial amount of graduate level mathematics (though my PhD is in Optical Physics, so I don't have quite enough math-specific classes for a graduate degree in that field). I have also been a math teacher.
First, the easy one: e_i_pi was slightly off in his discussion of plank lengths as a counter example of nonexistance of infinitesimals. The reason is that the set of real numbers is dense - meaning that between any two distinct real numbers there exists at least one (and actually an infinite amount) of other distinct real numbers. This is not so in the physical world. Consider two different lengths: 1 plank length and 2 plank lengths. Those are clearly distinct lengths, but there is no measurable length that is strictly between the two.
Also, 0 is most definitely a number. It is a member of the sets of natural numbers, integers, rational number, real numbers, and complex numbers. It is essential to all of these number sets in order to provide a complete definition for the addition operation (it is the identity element with respect to addition in most number systems).
Now then, it is quite clear that Prowler doesn't understand the concept of infinity. But I think the problem he is having is that he is approaching mathematics from the computer programming side rather than from the abstract side (I do quite a bit of programming, so I think I understand why he's reaching the conclusions he is). The misconception is that 0.999... is either a series approaching some value, or that it is lacking in some way. It isn't either. It is an exact number with an exact value. Certainly the "..." gives our brains some trouble (and our computers even more trouble!), but it is a notation that has an exact value and an exact meaning. Likewise 2/infinity and 1/infinity are not limits in and of themselves. lim(1/x, x->inf) and lim(2/x, x->inf) are limits and are absolutely not the same as 1/infinity and 2/infinity. But also note that the two limits have the same value. It doesn't matter than one is smaller than the other for all values of x, both limits have the exact same value! If you want to take about the rate at which they approach 0, we can discuss derivatives, but the concept of interest is the value of 1/x "at infinity", and when we use the limit to express that, we find that it is exactly the same value as 2/x regardless of which one is getting there quicker. (I started to say "gets there first," but that has no meaning when both only get there at infinity anyway. Better to say they get there at the same time.)
It is true that infinity is not a real number, but it can be used as a number if done carefully (see Definition 2.2 - the extended real number system on page 23 of "Introductory Real Analysis by Dangello and Seyfried). The problem Prowler is having is in thinking that infinity+1 is larger than infinity. This is a necessary condition in order for 1 - 0.99999... > 0. However, it is a flawed premise, and I can provide you a proof using the concept of cardinality.
Cardinality is the size of a set of numbers - think of it as the number of numbers in a set. So the cardinality of the set {0,1} is 2, while the cardinality of {1,2,3} is 3. That two sets have the same cardinality is equivalent to the two sets having a mapping between them that is both "one-to-one" and "onto." In simplified terms, if I have two sets and I can provide a direct mapping between every element in one set to a distinct element in the other set and vice versa, the sets are said to have the same cardinality. For example, {1,2,3} is easily mapped to {1,2,5}. In some cases we can express the mapping as a convenient formula: {1,2,3} maps to {2,4,6} using the formula y=2x. Natural numbers is the set including 0 and all positive integers: {0,1,2,3,4,5,...}. What is the cardinality of this set? It is clearly infinite, and its cardinality of this set is called Aleph Null. Any set for which one can find an exact 1-to-1 mapping with the natural numbers is said to be "countable infinite" and has a cardinality of Aleph Null. Conversely, if you have a set that contains every natural number but for which it is impossible to map every one of its elements to a distinct natural number, this set has a larger cardinality.
Here's where things get really funny. Consider the set, A, which contains all the natural number (N), and the number -1. So, A = {-1,0,1,2,3,4,...}. If the cardinality of N is inifinite (Aleph Null), logic would suggest that the cardinality of A is (Aleph Null + 1). That would actually be incorrect. Consider the mapping: a=n-1. (Where a is a member of A and n is a member of N). For every single member a, there exists a corresponding member, n, and vice versa. This mapping is both 1-to-1 and onto. The two sets have the same cardinality, and infinity+1=infinity.
It is straightforward to show that the cardinality of the positive even integers is the same as the positive integers, and that the cardinality of all integers {...,-2,-1,0,1,2,3,...} is likewise the same (for some additional fun on all this, look up Hilbert's Hotel). Furthermore, it is possible to show that the set of rational numbers (all numbers that can be expressed as a/b where a,b are members of the set of integers) likewise has the same cardinality as the natural numbers. This is an extremely interesting result because the rational numbers are dense, while the natural numbers are not! On the other hand, the real numbers are dense but are uncountable (which was proved by Georg Cantor in 1874). The cardinality of the real numbers is believed to be Aleph 1 (think of it as the next larger value of infinity). I won't get into all the details. Real numbers have a larger cardinality than the naturals, and that cardinality is supposed to be the same as the cardinality of the so-called power set of the natural numbers, but this hypothesis can be neither proved nor disproved.
The point of all this is about the size of infinity. There are in fact multiple values of infinity (aleph null, aleph 1, aleph 2, ...), however, you don't increase the size of a set from one level to the next by simply adding a finite number of elements. Nor can you do it even by squaring the number of elements. It might be best to think of the relations between them as being on the order of the factorial operation. This isn't strictly valid, but it's convenient to think about the relative sizes in this way.
Now that I've explained all that (and clearly demonstrated a sufficient feel for the concept of infinity), let's go back to the original problem. It is a definition of real numbers that if two numbers are distinct, there exists some number (that is a member of the real numbers) strictly between them. Note that if a number is a member of the reals, it has to be represented as such either as a truncated or repeating decimal (in which case it is a rational number and can also be written as a fraction of integers) or as an infinite non-repeating decimal (in which case it is irrational and may not be written with perfect precision but can be written as an approximation with arbitrary precision). 0.9 and 1 are clearly distinct - 0.95 is strictly between them. 0.99 and 1 are distinct - 0.995 is strictly between them. The question is whether 0.99... and 1 are distinct. What possible real number can fall between them? The previous two examples might lend someone to suggest (and I've seen people on other forums try this) that 0.999...9995 could be somehow larger than 0.999... Yet this is simply impossible. This claim requires that you somehow be able to affect the infinity+1 digit without changing the infinity digit. Furthermore, 0.999...9995 really has no meaning except as a finite decimal, in which case it is actually less than 0.999...! Likewise, there is no such thing as 0.00.....001 except as a very small finite number. If you try to posit that there is such a number, you should be ready to explain what digit follows the 1! And if you try to work with the 0.999...995 once more, I'll ask you to name the digit that contains the 5, and I'll let my 0.999... have a 9 in that digit and another 9 for infinite digits beyond the one containing your 5. My number will be larger than yours and has no difference between it and 1.
- TheProwler
- Posts: 354
- Joined: Mon Feb 12, 2007 9:54 am
- Gender: Male
- Location: Ontario, Canada
Re: .999... = 1
Dude, you are using "infinity" to get it...are you just joking?a.sub wrote:am i being ignored here? here is an example where you get .9999999...sully800 wrote:That's strange, because I use and see the number 1 all the time. In fact I think I use it more than any other number!TheProwler wrote:As I've said months ago, this is such a silly discussion because you will never come across the "number" 0.999... in mathematics (or in real life)
El Capitan X wrote:The people in flame wars just seem to get dimmer and dimmer. Seriously though, I love your style, always a good read.
Re: .999... = 1
Another quick thought (which a.sub reminded me of with his summation example):
It can be shown (see any Algebra 2 textbook) that a repeating decimal can be written as a rational number. In fact, there is a cute little trick you can use to write the rational representation quickly. Assume that the sequence of number that repeats contains N digits (0.1111.... has 1 repeating digit, 0.212121212... has 2 repeating digits, 0.314314314314... has 3 repeating digits, and so on). Take those N digits and put them in the numerator of your fraction. The denominator is exactly given as a number containing N 9s. The three above examples can all be written as 1/9, 21/99, 314/999 respectively.
To prove this, you can use the same proofs that have been presented elsewhere in this thread, or you can use the definition for the sum of an infinite geometric series. Recall that the sum is an approximation for a large number of terms in the series, but it is exact when you include infinite terms.
The upshot is that 0.999... can be written (exactly) as 9/9 or 99/99 or 999/999, etc... All of these are exactly equal to 1.
I'd also point out that I (and others) can cite published mathematical texts that assume, prove, and even require that 0.999...=1. Prowler has essentially said, "No it's not, and no one else understands why but me." For his claims to be valid, one of two things has to happen. Either there is a group of respected mathematicians that would agree with his claims (and I would like to see documented proof of this) or he is the first to prove his claims, in which case he deserves to win the Field's Medal!
It can be shown (see any Algebra 2 textbook) that a repeating decimal can be written as a rational number. In fact, there is a cute little trick you can use to write the rational representation quickly. Assume that the sequence of number that repeats contains N digits (0.1111.... has 1 repeating digit, 0.212121212... has 2 repeating digits, 0.314314314314... has 3 repeating digits, and so on). Take those N digits and put them in the numerator of your fraction. The denominator is exactly given as a number containing N 9s. The three above examples can all be written as 1/9, 21/99, 314/999 respectively.
To prove this, you can use the same proofs that have been presented elsewhere in this thread, or you can use the definition for the sum of an infinite geometric series. Recall that the sum is an approximation for a large number of terms in the series, but it is exact when you include infinite terms.
The upshot is that 0.999... can be written (exactly) as 9/9 or 99/99 or 999/999, etc... All of these are exactly equal to 1.
I'd also point out that I (and others) can cite published mathematical texts that assume, prove, and even require that 0.999...=1. Prowler has essentially said, "No it's not, and no one else understands why but me." For his claims to be valid, one of two things has to happen. Either there is a group of respected mathematicians that would agree with his claims (and I would like to see documented proof of this) or he is the first to prove his claims, in which case he deserves to win the Field's Medal!
- TheProwler
- Posts: 354
- Joined: Mon Feb 12, 2007 9:54 am
- Gender: Male
- Location: Ontario, Canada
Re: .999... = 1
"if done carefully"Doc_Brown wrote:It is true that infinity is not a real number, but it can be used as a number if done carefully (see Definition 2.2 - the extended real number system on page 23 of "Introductory Real Analysis by Dangello and Seyfried).
I played hockey with a guy. One time, I wasn't there, he was playing with a small explosive device and it blew off one of his fingers. And he was careful.
People that are careful still make mistakes.
Or, that infinity-1 is smaller than infinity.Doc_Brown wrote:The problem Prowler is having is in thinking that infinity+1 is larger than infinity.
But let's have a good laugh at that!!! Because we all understand infinity, right!!
A "proof" using a "concept".Doc_Brown wrote:I can provide you a proof using the concept of cardinality.
Interesting.
You see the problem, right?
This whole "problem" is just a good example of why that definition is flawed.Doc_Brown wrote:Now that I've explained all that (and clearly demonstrated a sufficient feel for the concept of infinity), let's go back to the original problem. It is a definition of real numbers that if two numbers are distinct, there exists some number (that is a member of the real numbers) strictly between them.
We are not talking about man's definition of numbers. We aren't even talking about reality. 0.999... is not real. Sure, it's a real number, but it is not real. We are talking about a "number" that can only conjured up by misapplying arithmetic to numbers that are estimates or by creating sequences that involve infinity.
Oh!! The old "My number is larger!!" game.Doc_Brown wrote:Note that if a number is a member of the reals, it has to be represented as such either as a truncated or repeating decimal (in which case it is a rational number and can also be written as a fraction of integers) or as an infinite non-repeating decimal (in which case it is irrational and may not be written with perfect precision but can be written as an approximation with arbitrary precision). 0.9 and 1 are clearly distinct - 0.95 is strictly between them. 0.99 and 1 are distinct - 0.995 is strictly between them. The question is whether 0.99... and 1 are distinct. What possible real number can fall between them? The previous two examples might lend someone to suggest (and I've seen people on other forums try this) that 0.999...9995 could be somehow larger than 0.999... Yet this is simply impossible. This claim requires that you somehow be able to affect the infinity+1 digit without changing the infinity digit. Furthermore, 0.999...9995 really has no meaning except as a finite decimal, in which case it is actually less than 0.999...! Likewise, there is no such thing as 0.00.....001 except as a very small finite number. If you try to posit that there is such a number, you should be ready to explain what digit follows the 1! And if you try to work with the 0.999...995 once more, I'll ask you to name the digit that contains the 5, and I'll let my 0.999... have a 9 in that digit and another 9 for infinite digits beyond the one containing your 5. My number will be larger than yours and has no difference between it and 1.
That seems like a joke. But re-read the last paragraph. "And if you try to work with the 0.999...995 once more, I'll ask you to name the digit that contains the 5, and I'll let my 0.999... have a 9 in that digit and another 9 for infinite digits beyond the one containing your 5." That's just getting a little silly.
El Capitan X wrote:The people in flame wars just seem to get dimmer and dimmer. Seriously though, I love your style, always a good read.
- ser stiefel
- Posts: 48
- Joined: Wed Apr 25, 2007 4:21 pm
- Gender: Male
Re: .999... = 1
Well, thanks Doc Brown for taking the fun out of reading the arguments posted here. 
Nothing like having someone who actually knows what he is talking about to spoil a good show. The good news is few enough people will be interested in digesting your post to get anything out of it! So the argument will likely continue!
So the argument will likely continue!
I have a BA in math (was a math teacher for a while too), and it was in a few graduate level courses that I discovered I was probably not cutout to work on a PhD in mathematics. Elementary Topology as an elective proved more work for me than I wanted (or was able, I am not to embarrassed to admit) to do. I dropped it after about 3 weeks. The only class I ever dropped. Ah well.
Nothing like having someone who actually knows what he is talking about to spoil a good show. The good news is few enough people will be interested in digesting your post to get anything out of it!
I have a BA in math (was a math teacher for a while too), and it was in a few graduate level courses that I discovered I was probably not cutout to work on a PhD in mathematics. Elementary Topology as an elective proved more work for me than I wanted (or was able, I am not to embarrassed to admit) to do. I dropped it after about 3 weeks. The only class I ever dropped. Ah well.
The Tick wrote:How dare you! I know evil is bad, but come on! Eating kittens is just plain... plain wrong, and no one should do it! EVER!
Re: .999... = 1
And yet this was an accepted definition in a respected graduate level mathematics text. You still haven't backed up any of your arguments with published works.TheProwler wrote: "if done carefully"
I played hockey with a guy. One time, I wasn't there, he was playing with a small explosive device and it blew off one of his fingers. And he was careful.
People that are careful still make mistakes.
The proof that a+b=b+a for all a,b contained in the set of natural numbers relies on the concept of mathematical induction. In fact, many mathematical proofs rely on definitions and concepts. You have had a mathematical proofs course, yes?TheProwler wrote:A "proof" using a "concept".Doc_Brown wrote:I can provide you a proof using the concept of cardinality.
Interesting.
You see the problem, right?
This is only partly true. Repeating infinite decimals are real numbers in every sense of the word. Furthermore, they are every bit as precise as their rational number representations. It is true that non-repeating infinite decimals are imprecise, but 0.99... is one of the former, not the later. It is no less precise than the sum of an infinite series (which has to be precise or the entire field of calculus is incorrect, or didn't you know that the integral formulas are only valid because they rely on the exact value of infinite sums?). Algebra was nowhere misapplied in producing 0.999... (except where you try to claim that one value of 0.333... is less than another value of 0.333...). Certainly infinite series can be used to produce it, but that doesn't invalidate its existence. What about phi (the golden ratio). I can produce it using the method of continued fractions. Does that make it invalid even though it shows up repeatedly throughout nature?TheProwler wrote:This whole "problem" is just a good example of why that definition is flawed.
We are not talking about man's definition of numbers. We aren't even talking about reality. 0.999... is not real. Sure, it's a real number, but it is not real. We are talking about a "number" that can only conjured up by misapplying arithmetic to numbers that are estimates or by creating sequences that involve infinity.
Of course it's getting silly. I was trying to highlight the absurdity in trying to define a number strictly between 0.99... and 1.TheProwler wrote:Oh!! The old "My number is larger!!" game.
That seems like a joke. But re-read the last paragraph.That's just getting a little silly.Doc_Brown wrote:"And if you try to work with the 0.999...995 once more, I'll ask you to name the digit that contains the 5, and I'll let my 0.999... have a 9 in that digit and another 9 for infinite digits beyond the one containing your 5."
Just to point out, the majority of this post I'm quoting from was more ad hominem than actual fact. I, and others, have cited a variety of mathematical texts to support our arguments. I'm still waiting to see any source material to back up your claims (apart from your programming instructor at the University years ago, whose comments you may or may not remember precisely). If you're simply trolling, I commend you. Well done to keep this going for 23 (24 now?) pages and stretching nearly a year now!
Re: .999... = 1
Yeah. I wasn't especially keen on the more abstract side of mathematics either. I really enjoyed proofs, if only because I only ever had to memorize a few basic concepts and I could re-derive everything else I might need. I also enjoyed the foundations and real analysis classes, but I avoided the geometry and topology electives. I went with PDEs, Fourier Analysis, Numerical Methods, Mathematical Modeling, Complex Analysis, and the like. But then, I'm more of a physics guy at heart anyway. Mathematics was originally developed as a means of describing nature, and that's what physics is at its heart: the mathematical description of the world. In some ways, upper level theoretical physics is really all about determining the appropriate differential equation to describe some phenomenon, and then solving it to predict behavior. It's a lot of fun really!ser stiefel wrote:Well, thanks Doc Brown for taking the fun out of reading the arguments posted here.
Nothing like having someone who actually knows what he is talking about to spoil a good show. The good news is few enough people will be interested in digesting your post to get anything out of it!So the argument will likely continue!
I have a BA in math (was a math teacher for a while too), and it was in a few graduate level courses that I discovered I was probably not cutout to work on a PhD in mathematics. Elementary Topology as an elective proved more work for me than I wanted (or was able, I am not to embarrassed to admit) to do. I dropped it after about 3 weeks. The only class I ever dropped. Ah well.
- ser stiefel
- Posts: 48
- Joined: Wed Apr 25, 2007 4:21 pm
- Gender: Male
Re: .999... = 1
haha.. I remember when I was in junior college, my major was computer science and I met a guy whose major was math and I remember thinking," what strange major." Then several years later, I went back to school with math as my major! Never know where life will lead. Real Analysis was interesting to me also, was the first time I had been introduced such ideas. Applied Combinatorics was the most fun for me. I was fortunate to have the chair of the math dept at Iowa as my instructor for that one. A really brilliant guy. I recall he was doing some work in advanced algebra systems involving "buildings". Still don't know what he was talking about!Doc_Brown wrote:Yeah. I wasn't especially keen on the more abstract side of mathematics either. I really enjoyed proofs, if only because I only ever had to memorize a few basic concepts and I could re-derive everything else I might need. I also enjoyed the foundations and real analysis classes, but I avoided the geometry and topology electives. I went with PDEs, Fourier Analysis, Numerical Methods, Mathematical Modeling, Complex Analysis, and the like. But then, I'm more of a physics guy at heart anyway. Mathematics was originally developed as a means of describing nature, and that's what physics is at its heart: the mathematical description of the world. In some ways, upper level theoretical physics is really all about determining the appropriate differential equation to describe some phenomenon, and then solving it to predict behavior. It's a lot of fun really!ser stiefel wrote:Well, thanks Doc Brown for taking the fun out of reading the arguments posted here.
Nothing like having someone who actually knows what he is talking about to spoil a good show. The good news is few enough people will be interested in digesting your post to get anything out of it!So the argument will likely continue!
I have a BA in math (was a math teacher for a while too), and it was in a few graduate level courses that I discovered I was probably not cutout to work on a PhD in mathematics. Elementary Topology as an elective proved more work for me than I wanted (or was able, I am not to embarrassed to admit) to do. I dropped it after about 3 weeks. The only class I ever dropped. Ah well.
The Tick wrote:How dare you! I know evil is bad, but come on! Eating kittens is just plain... plain wrong, and no one should do it! EVER!
- sully800
- Posts: 4978
- Joined: Wed Jun 14, 2006 5:45 pm
- Gender: Male
- Location: Bethlehem, Pennsylvania
Re: .999... = 1
Doc, don't get sucked into Prowler's nonsense. Some people argue for the sake of achieving a better understanding, but that is not his quest. I don't even believe it is a quest to insist that his belief is correct while everyone else is wrong. Rather, he starts with the assumption that everyone else is wrong and makes his belief the opposite simply to have a point to argue.
Thank you Prowler for making my day and vehemently resuming this discussion where it was left months ago. I hope "0.999..." day we can all look back on this and laugh. I know I will!
Thank you Prowler for making my day and vehemently resuming this discussion where it was left months ago. I hope "0.999..." day we can all look back on this and laugh. I know I will!
